Michael Neuhold Homepage
Startseite > Geographie > Addenda zur Geschichte der Landkarte

Addenda zur Geschichte der Landkarte

• Mein Verhältnis zur Geographie
• Äquator, Meridian, Wendekreis, Polarkreis
  • Äquator
  • Wendekreis
  • Polarkreis
  • Meridian
  • Nullmeridian
  • Orthodrome
  • Loxodrome
  • Zenit
  • Nadir
  • Azimut
• Wo bin ich gerade?
  • Geographische Breite
  • Geographische Länge
  • Triangulation
• Projektion
  • Azimutalprojektionen
  • Zylinderprojektionen
  • Kegelprojektionen
• Karten als Ausdruck der Weltsicht
• Warum ist Norden oben?
• Kartendruck
  • Holzschnitt
  • Kupferstich
  • Lithographie
  • Offsetdruck
• Beachtenswerte frühe Karten
  • Babylonische Weltkarte
  • Soleto-Karte (Mappa di Soleto)
  • Tabula Peutingeriana
  • Mosaik von Madaba
  • T-O-Karten
    • Beatuskarte
    • Ebstorfer Weltkarte
    • Hereford-Karte
    • Karte des Fra Mauro
  • Portolankarten
  • Lucas Cranachs Karte des Heiligen Landes
• Seltsame Orte
  • Thule
  • Säulen des Herakles
  • Kap der Guten Hoffnung
  • Inseln der Seligen
  • Syrte

Mein Verhältnis zur Geographie

Der Duden empfiehlt die Schreibung Geograf, -grafie, -grafisch, ebenso bei Karto-, Litho-, Ortho-, Fotograf. Ich schreibe hier durchgehend -graph, inkonsequenterweise allerdings Grafik. Anhänger der Dudenschreibung mögen über meine ältertümelnde Orthographie hinwegsehen.

Es gereicht dem Unterrichtsfach Geographie nicht zum Vorteil, dass es so häufig von „Sportographen“ unterrichtet wird, Sportwissenschaftlern, die offenbar ein zweites Fach gebraucht haben (so ist es in Österreich, von wenigen Ausnahmen abgesehen, für Lehramtskandidaten vorgeschrieben), aber nicht wirklich große Begeisterung für die Geographie haben. Zumindest haben meine Geographielehrer, wie ich finde, überwiegend Dienst nach Vorschrift gemacht. So musste ich so geistlose Dinge lernen, wie alle Zuflüsse der Donau in Oberösterreich oder die Namen der Bergketten in den Alpen (Ötztaler Alpen, Stubaier Alpen, Zillertaler Alpen usw.). Auch die Wirtschaftsgeographie oder die Geologie erfuhren dieselbe Behandlung (ich weiß bis heute nicht, was eine Flyschzone ist). So war es kein Wunder, dass ich Geographie immer langweilig fand und darin auch schlechte Noten heimbrachte.

Ein leises Interesse für Geographie erwachte bei mir erst durch die Beschäftigung mit dem geographischen Wissen des Altertums (s. z.B. meine Seiten Die Völkertafel (Gen 10), Jawan & Söhne, Eden, oder das Lehrbuch der Alten Geographie von Heinrich Kiepert bei Archive.org). Wie wichtig Geographie sein kann, wurde mir auch durch einige Folgen der Dokumentarreihe Mit offenen Karten, die ich auf Youtube gesehen habe, klar.

Dann habe ich zwei Bücher zu diesem Thema gelesen, J. Blacks Geschichte der Landkarte und J. Harwoods Hundert Karten die die Welt veränderten, war aber enttäuscht. Beide Werke überzeugen zwar durch modernes Bildmaterial, reduzieren die Geschichte der Landkarte aber im großen und ganzen auf die langatmige Darstellung der Geschichte der Entdeckung der Welt und der Zunahme unseres geographischen Wissens. Andere Themen, wie immer ausgeklügeltere Kartenprojektionen oder die Verbesserung von Techniken des Buchdrucks, werden nur en passant erwähnt. Viele Dinge werden überhaupt nicht erklärt. (Was hat die Navigation auf See eigentlich mit der Uhr zu tun?)

Wesentlich aufschlussreicher war die Lektüre von V. Oswalts Weltkarten – Weltbilder. Aber auch Oswalt setzt kartographisches Grundwissen voraus. Ähnlich im Gehalt, aber viel ausführlicher ist J. Brottons Geschichte der Welt in zwölf Karten.

Ich habe ein paar „Randthemen“ auf eigene Faust recherchiert und gebe hier eine kurze Zusammenfassung. Das ganze ist ein unsystematisches Sammelsurium zum Thema Kartographie.

Äquator, Meridian, Wendekreis, Polarkreis

rot: Äquator, grün: Meridian von Greenwich.
Urheber: Wikipedia-User Cham.– Quelle: Wikimedia.– Lizenz: GFDL 1.2, CC BY-SA 3.0.– Bearbeitung: verkleinert, Äquator und Nullmeridian eingefärbt.

Die Erde zur Sommer­sonnen­wende. Die Erdachse ist um einen Winkel ε (ca. 23° 27') gegenüber der Ebene des Umlaufs um die Sonne geneigt. Dadurch ergeben sich die besonderen Breitenkreise (Wendekreise, Polarkreise).
Urheber: cmglee, NASA.– Quelle: Wikipedia.– Lizenz: gemeinfrei.– Bearbeitung: vereinfacht und ins Dt. übersetzt.

grün: Orthodrome (kürzester Weg), blau: Loxodrome (winkel­konstanter Kurs) von A nach B.
Urheber: Wikipedia-User McSush.– Quelle: Wikimedia.- Lizenz: CC BY-SA 2.5.– Bearbeitung: Kurven eingefärbt, verkleinert.

Äquator

v. lat. aequātor „Gleichmacher, Eicher“

Größter Kreis, dessen Ebene senkrecht zur Erdachse steht; er teilt die Erde in eine Nord- und eine Südhalbkugel (daher der Name). Der Äquator hat die geographische Breite 0 und ist Bezugspunkt für die parallel zu ihm verlaufenden Breitenkreise.

Wendekreis (des Krebses, des Steinbocks)

engl. tropic, v. lat. tropicus = griech. τροπικός „Wende-“ (erg. circulus „Kreis“)

Die beiden Breitenkreise ca. 23° 26′ nördlicher und südlicher Breite. Innerhalb dieses Bereichs (den sog. Tropen) erreicht die Sonne den Zenit, auf den Wendekreisen nur einmal im Jahr (im Norden am Tag der Sommersonnenwende). Da sich die Neigung der Erdachse dauernd ändert, verschieben sich die Wendekreise um ca. 14 m pro Jahr. Das Sternbild, das die Sonne nördlich des Äquators zur Sonnenwende durchquerte, war bis 15 v.Chr. das Sternbild Krebs, daher der Name des Wendekreises.

Polarkreis

Die beiden Breitenkreise ca. 66° 34′ nördlicher und südlicher Breite. In den Gebieten jenseits der Polarkreise (den Polarregionen) geht die Sonne mindestens einmal im Jahr (im Norden zur Sommersonnenwende) nicht ganz unter (Mitternachtssonne) und einmal (zur Wintersonnenwende) nicht auf. Die Zeit, in der die Sonne nicht auf- bzw. untergeht wird umso länger, je mehr man sich den Polen nähert. Direkt an den Polen ist es ein halbes Jahr lang Tag, ein halbes Jahr lang Nacht (mit mehrwöchigen Dämmerungsperioden dazwischen).

Meridian

v. lat. (circulus) merīdiānus „Mittagskreis“

Halbkreis von Pol zu Pol; Längenkreis (alle Ort darauf haben die gleiche geographische Länge); Linie aller Orte, an denen gleichzeitig Mittag ist (daher der Name).

Ein Meridian ist ziemlich genau 20.000 km lang. Das ist kein Zufall: der Meter war ursprl. definiert als der zehnmillionste Teil des (kürzesten) Abstands von Pol zu Äquator. In der Seefahrt rechnet man allerdings in nautischen Meilen (auch Seemeilen genannt). 1 nm entspricht 1 Bogenminute am Meridian oder am Äquator, das wären zwischen 1843 und 1862 m. International festgelegt wurde sie mit 1852 m. Aber für die Zwecke der Navigation ist die Definition mit der Bogenminute ausreichend genau, die exakte Länge ist irrelevant.

Für eine volle Drehung um die eigene Achse (360°) braucht die Erde im Mittel 23 Std. 56 Min. 4 Sek. (ein siderischer Tag). In einer Stunde dreht sie sich um 15,04°. Das sind am Äquator gut 1664 km!

Nicht verschwiegen werden soll, dass der Wikipedia-Art. Längenproblem (Stand Mai 2016) von einer Drehung von 360° innerhalb von 24 Std. ausgeht. Ich bin mir nicht sicher, ob ich einem Denkfehler erlegen bin oder der Wikipedia-Autor.

Nullmeridian

Da es keinen per se bevorzugten Meridian gibt, ist die Definition des Meridians mit der geographischen Länge 0 eine reine Festlegung. Ursprünglich hatte jedes größere Land seinen eigenen Nullmeridian. Historisch bedeutsam sind etwa der schon von Ptolemäus verwendete Meridian von Ferro (heute El Hierro, die westlichste der Kanarischen Inseln), der westlichsten zu Ptolemäus' Zeit bekannten Landmasse. Ein anderer wichtiger Meridian war der Meridian von Paris. Als 1884 die Internationale Meridian-Konferenz abgehalten wurde, basierte aber bereits der überwiegende Teil der Seekarten auf dem Meridian, der durch die Sternwarte im Londoner Stadtteil Greenwich geht. Daher setzte sich der Greenwich-Meridian mit klarer Mehrheit durch.

Der Meridian, der durch das Pariser Observatorium geht, ist vor allem durch Dan Browns Buch Sakrileg (engl. Titel The Da Vinci Code, 2003) bekannt geworden. Brown hat für ihn den Namen „Rosenlinie“ erfunden. Der Mittagsweiser mit dem sog. Gnomon in der Kirche Saint-Sulpice liegt aber nicht, wie im Buch behauptet, auf diesem Meridian, sondern lediglich in seiner Nähe.

Der Meridian von Greenwich wurde ursprünglich über astronomische Bezugspunkte (Durchgang von Sternen durch den Meridian zu einer bestimmten Zeit) definiert. Doch offenbar gab es dabei infolge einer Gravitationsanomalie einen Lotfehler. Die Anwendung der Definition führt dazu, dass der heutige Nullmeridian gut 100 m östlich des historischen Meridians von Greenwich verläuft. Doch ist der Nullmeridian heute ohnedies nicht mehr über einen bestimmten Ort auf der Erdoberfläche definiert. Dies wäre zu ungenau, da sich Ortslagen durch Kontinentalverschiebung laufend ändern, die Pole sich jährlich um einige Meter bewegen und die Erdoberfläche sich durch Gezeitenkräfte ständig verformt. Der Nullmeridian ist daher heute über geodätische terrestrische Referenzmodelle (GRS-80, WGS 84, ETRS89, ITRS) definiert.

Orthodrome

v. griech. ὀρθός ort^hós „gerade“, δρομή dromḗ = δρόμος drómos „Lauf“

Kürzeste Verbindung zweier Punkte auf der Erdkugel, also das, was man landläufig Luftlinie nennt.

Loxodrome (Schiefläufige)

v. griech. λοξός loxós „schief, schräg“

Kurve, die alle Meridiane im gleichen Winkel schneidet, daher auch Winkelgleiche genannt. Von den zwei Sonderfällen – Schnittwinkel 0° (Loxodrome ist ein Meridian) und Schnittwinkel 90° (Loxodrome ist ein Breitenkreis) – abgesehen ist die Loxodrome eine Kurve, die sich spiralig um den Globus windet.

Wenn man bei der Navigation mit Kompass immer einen konstanten Winkel einhält, folgt man einer Loxodrome. Da in mittleren Breiten die Loxodrome nur ungleich länger ist als die Orthodrome, wurde sie jahrhundertelang zur Navigation auf See verwendet. Navigation nach der Orthodrome erfordert konstante Veränderung des Kompasswinkels, dazu muss man zu jedem Zeitpunkt exakt wissen, wo man sich befindet, was ohne GPS schwierig ist.

Vor der Einführung von winkeltreuen Karten bediente man sich u.a. des Segelns auf Großkreisen, d.h. man segelte auf Breitenkreisen und Meridianen, bei denen Orthodrome und Loxodrome identisch sind, man also nach einem konstanten Kompasswinkel segeln konnte.

Zenit

v. arab. (سمت (الرأس samt (ar-raʾs) wörtl. „Weg (des Kopfes)“

Scheitelpunkt des Himmelsgewölbes

Nadir (der)

v. arab. نظير naẓīr „entsprechend, gegenüberstehend; Gegenstück“

der dem Zenit gegenüberliegende Fußpunkt

Azimut (das od. der)

v. arab. السموت as-sumūt „die Wege“ (Sg. سمت samt)

Horizontalwinkel; in der Kartographie der Winkel zwischen dem geographischen Norden und der Marschrichtung (im Uhrzeigersinn gemessen, d.h. Osten = 90°).

Wo bin ich gerade?

Späte Sühne ist ein Film mit Humphrey Bogart aus dem Jahr 1947, der englische Originaltitel lautet Dead Reckoning. Ich habe im Langenscheidt nachgeschaut, was das eigentlich heißt: „gegißtes Besteck“. Da war ich zunächst ratlos. Die Lösung: Als Besteck bezeichnet man in der Seefahrt die Bestimmung der eigenen Position. Gissung, gissen bedeutet „schätzen“. Gegisstes Besteck ist die Schätzung der aktuellen Position ausgehend vom letzten Startpunkt an Hand der eingeschlagenen Richtung und der vermutungsweise zurückgelegten Strecke (Fahrtzeit mal geschätzte Geschwindigkeit). Ein verständlicherer Ausdruck dafür ist Koppelnavigation. Der englische Filmtitel ist ein Wortspiel, denn reckoning heißt auch „Abrechnung“.

Im folgenden werden nur prinzipielle Möglichkeiten für die nördliche Hemisphäre dargelegt. Für praktische Zwecke geht man anders vor (s.u.) und berücksichtigt Details wie Kimmhöhe, Refraktion und Parallaxe. Ich bin bei diesem Thema ein reiner Theoretiker. Ich gehe davon aus, dass niemand so lebensmüde ist, im Vertrauen auf meine Ausführungen zu navigieren. Aber wer einen Sextanten benützen kann, wird es ohnehin besser wissen als ich.

Geographische Breite

Bestimmung der Breite mit dem Polarstern.

Bestimmung der Mittagsbreite: 𝛼 = gemessener Höhenwinkel, 𝛿 = Deklination der Sonne.

Funktionsweise eines Quadranten: man visiert über die Ober­kante ein Objekt an (roter Pfeil), das Lot (grüner Pfeil) zeigt auf einer Grad­skala den Höhen­winkel 𝛼.– Urheber: Michael Daly, 2007.– Quelle: Wikimedia.– Lizenz: GFDL, CC BY-SA 3.0.– Bearbeitung: verkleinert neu gezeichnet, Himmels­objekt und Skalen­beschriftung hinzugefügt.

Am einfachsten ist auf der Nordhalbkugel die Bestimmung der Polhöhe mit Hilfe des Polarsterns, der fast genau auf dem Himmelsnordpol liegt. Der Höhenwinkel (auch Vertikalwinkel genannt) des Himmelspols ist identisch mit der geographischen Breite. (Für eine ernsthafte Ortsbestimmung muss man den Abstand des Sterns vom Himmelspol zum Zeitpunkt der Messung, die man einem nautischen Almanach entnehmen kann, dazuaddieren.)

Man kann auch jeden anderen Stern nehmen und seinen Höhenwinkel zum Zeitpunkt seiner oberen Kulmination (d.h. wenn er seinen höchsten Stand am Himmel erreicht hat) – oder anders gesagt: wenn der Stern genau im Süden steht – messen. Dann muss man seinen Abstand vom Himmelspol dazurechnen, d.h. 90 - Deklination δ. (Die Deklination ist die geographische Breite des Sterns auf der Himmelskugel.) Die so bestimmte Breite wird Meridianbreite genannt. (In der Astronomie wird als (Himmels-)Meridian jener Großkreis am Firmament bezeichnet, der vom Nordpunkt des Horizonts durch den Zenit zum Südpunkt geht.)

Eine andere Methode ist die Bestimmung der Mittagsbreite. Dazu wird der Höhenwinkel der Sonne zum Zeitpunkt ihrer oberen Kulmination gemessen (dieser Zeitpunkt heißt auch Schiffsmittag) und die Deklination der Sonne dazuaddiert; das ist die geographische Breite, über der die Sonne an diesem Tag im Zenit steht. Wie oben unter Wendekreis dargelegt, dekliniert die Sonne zwischen den beiden Wendekreisen und steht nur zweimal im Jahr, nämlich zu den Äquinoktien (Frühlings- und Herbstbeginn), genau über dem Äquator im Zenit (Deklination 0). An diesen beiden Tagen ist die Zenitdistanz identisch mit der geographischen Breite und die Sonne kulminiert genau im Süden.

In der Praxis geht man folgendermaßen vor (s. Astronomische Navigation bei Astrosail): Man misst den Höhenwinkel α eines astronomischen Objekts, z.B. am Taghimmel der Sonne, am Dämmerungs- oder Nachthimmel des Mondes, eines hellen Planeten wie der Venus oder eines geeigneten Gestirns. Aus einem nautischen Almanach kann man ersehen, über welcher geographischen Breite zum Messzeitpunkt dieses Objekt im Zenit stand. Die Differenz 90 - α definiert einen Kreis, auf dem man sich zum Zeitpunkt der Messung befand. Wenn man die Messung mit einem anderen Objekt oder bei der Sonne zu einem späteren Zeitpunkt wiederholt, ergibt sich ein zweiter Kreis. Die Schnittpunkte dieser beiden Kreise schränken die mögliche Position bereits auf zwei Punkte ein. Man misst den Höhenwinkel (den Winkel zum Horizont) und nicht die Zenitdistanz, weil der Horizont leichter zu bestimmen ist als der Zenit.

Kompassmissweisung, magnetische Deklination

Die Kompassnadel zeigt nicht zum geographischen Nordpol, also jenem Punkt, an dem die Erdachse „austritt“, sondern richtet sich entlang der magnetischen Feldlinien aus. Diese Feldlinien verlaufen aber nicht schnurgerade, sondern mit gewissen Abweichungen. Und der magnetische Nordpol, jener Punkt, von dem die Magnetfeldlinien ausgehen, liegt gut 800 km vom geographischen Nordpol entfernt und ändert seine Position auch ständig.

Refraktion

Die Lichtstrahlen von Sonne, Mond und Sternen werden von der Erdatmosphäre gekrümmt, sodass ihr Höhenwinkel größer erscheint, als er tatsächlich ist. Lediglich im Zenit (also bei genau senkrechten Einfallswinkel) ist die Refraktion 0. In Horizontnähe wird die Refraktion, abhängig von Temperatur und Luftdruck, manchmal so groß, dass Objekte über dem Horizont zu sehen sind, die sich in Wahrheit bereits hinter dem Horizont befinden.

Geographische Länge

Wie ermittelt man die geographische Länge? Es gibt ja keinen von Haus aus bevorzugten Meridian. Das ist das berühmt Längenproblem, von dem auch Umberto Eco in Die Insel des vorigen Tages ausführlich berichtet. Man nimmt eine genau gehende Uhr und eicht sie auf einen bestimmten Meridian, z.B. den Nullmeridian. (Wenn die Sonne über der Sternwarte von Greenwich ihren höchsten Punkt erreicht hat, stellt man sie auf 12 Uhr.) Wenn man nun nach etlichen Tagen Seefahrt feststellt, dass die Uhr zu Schiffsmittag (also wenn die Sonne ihren höchsten Punkt erreicht) 9:00 zeigt, weiss man, dass man 3 Stunden ~ 45,12 Längengrade vom Ausgangsmeridian entfernt ist.

Die Uhr muss wirklich genau gehen. Denn am Aquätor entsprechen 1 Minute Abweichung bereits fast 28 km. Daher war eine einfache Längenbestimmung auf See erst möglich, als es gelang, eine Uhr zu konstruieren, deren Ganggenauiggkeit vom Schwanken des Schiffes auf See nicht beeinflusst wurde (John Harrisons Schiffschronometer).

Die faktische Unmöglichkeit, die Länge genau zu bestimmen, führte im 16. Jh. zum Streit zwischen Portugal und Spanien. Die beiden Länder hatten im Vertrag von Tordesillas 1494 die Welt in eine portugiesische und eine spanische Hemisphäre aufgeteilt. Die Portugiesen entdeckten dann den Seeweg nach Indien (s.u. Kap der Guten Hoffnung), gelangten bis zu den Molukken und begannen den höchst lukrativen Gewürzhandel mit dieser Region. Als die unter spanischer Flagge segelnden Schiffe Magellans 1521 die Molukken von Westen her erreichten, behauptete Spanien, die Molukken befänden sich in ihrem Bereich. Beide Seiten legten Karten vor, auf denen die Molukken so verortet waren, dass sie in ihrer jeweiligen Hemisphäre lagen. Auf spanischer Seite waren es u.a. die Karten des aus Portugal gebürtigen Kartographen Diogo Ribeiro, die aber Unikate waren und nie gedruckt wurden. Am bekanntesten ist vermutlich Ribeiros Weltkarte Carta Universal von 1529. Im Vertrag von Saragossa verzichtete Spanien 1529 auf seine Ansprüche, und man einigte sich auf eine für beide Seiten verbindliche Karte. Diese ist aber nicht mehr erhalten.

Wegen der Unmöglichkeit, die aktuelle Länge zu bestimmen, betrieb man in der Seefahrt lange Zeit das sog. Breitensegeln. Man fuhr (mehr oder weniger) den aktuellen Meridian so lange nach Norden bzw. Süden, bis man sich auf der Breite des Zielorts befand. Dann fuhr man so lange auf diesem Breitenkreis nach Westen bzw. Osten, bis man den Zielort erreicht hatte. Davor betrieb man Küstenschifffahrt und orientierte sich auf offener See hauptsächlich an der Sonne.

Triangulation

Vermessung nach dem Triangu­lations­verfahren.

Ein wesentliches Verfahren zur Landvermessung ist die Triangulation. Eine Strecke zwischen zwei markanten Punkten wird (mit Messlatte, Messschnur o.ä.) so genau wie möglich vermessen. Dann wird von beiden Punkten aus ein drittes Objekte anvisiert und jeweils der Winkel zur gemessenen Grundlinie bestimmt. Man hat dann eine Seite c (=A̅B̅) und die drei Winkel (𝛼 und 𝛽, 𝛾 = 180°-𝛼-𝛽). Nach dem Sinussatz kann man dann die Länge der beiden anderen Dreiecksseiten ermitteln. Damit hat man zwei weitere Grundlinien, von denen aus man neue Punkte anvisieren kann. Die Landvermesser haben vom 17. bis zum 19. Jahrhundert mit diesem Verfahren das Land mit einem Netz von Dreiecken überzogen und so die Position von Orten und den Verlauf von Grenzen bestimmt.

Bsp.: A̅B̅ sei 5500 m, die Winkel zu C sind 65° und 75°, der dritte Winkel muss dann 40° betragen (Winkelsumme im Dreieck 180°). Nun gilt bekanntlich
c / sin 𝛾 = a / sin 𝛼 | · sin 𝛼
a = c / sin 𝛾 · sin 𝛼
a = 5500 m / 0,6428 · 0,9063 = 7754,8 m
(Alle Angaben ohne Gewähr. Diese Berechnung geht der Einfachheit halber davon aus, dass die drei Punkte in einer Ebene liegen. Bestehen zudem Unterschiede im Höhenniveau werden zusätzliche Rechenschritte notwendig.) Die Strecke B̅C̅ beträgt also 7754,8 m. Nach demselben Modus kann die dritte Stecke berechnet werden.

Projektion

Die Erde ist ein dreidimensionaler Körper, eine Karte ist zweidimensional. Um die Erdoberfläche „flachzudrücken“, gibt es verschiedene Möglichkeiten, Projektionen genannt. Jede Projektion muss die realen Verhältnisse verzerren. Eine Projektion kann winkeltreu, abstandstreu oder flächentreu sein, aber niemals alles zur gleichen Zeit. Heute verwendet man häufig Projektionen, die einen Kompromiss zwischen allen drei bieten.

Im Prinzip kann man die Kugeloberfläche auf eine Ebene projizieren (Azimutalprojektion), auf einen Zylindermantel oder auf einen Kegelmantel.

Azimutalprojektion	Zylinderprojektion	Kegelprojektion
Die Kartenfläche ist ein Kreis.	Die Kartenfläche ist ein Zylindermantel und daher immer rechteckig.	Die Kartenfläche ist ein Kegelmantel.

Azimutalprojektionen

Bei der orthographischen Azimutalprojektion werden die Punkte parallel projiziert. Dadurch wird die Erde so abgebildet, wie sie aus dem Weltraum zu sehen ist. (Jede Satellitenaufnahme der Erdoberfläche ist also eine Projektion auf die zweidimensiale Bildfläche.) Man kann damit natürlich nur eine Halbkugel abbilden. Bei der transversalen Projektion ist der Äquator der Mittelpunkt; bei transversaler orthographischer Projektion werden die Breitenkreise zu parallen Geraden. Bei der polaren Projektion ist ein Pol der Mittelpunkt; bei polarer orthographischer Projektion sind die Breitenkreise konzentrische Kreise. Es kann aber auch jeder andere Punkt der Erde als Mittelpunkt gewählt werden, man spricht dann von schiefer Projektion. Die orthographische Azimutalprojektion wurde bereits im 2. Jh. v.Chr. von Hipparchos von Nicäa verwendet. Bei der gnomischen Projektion werden die Punkte mit vom Erdmittelpunkt ausgehenden Strahlen projiziert. So kann man natürlich nicht die ganze Halbkugel abbilden, da die Strahlen, die parallel zur Abbildungsebene sind, diese nie treffen. Bei dieser Projektion wird die Orthodrome als Gerade abgebildet. Bei der stereographischen Projektion gehen die Strahlen von einem auf der Kugeloberfläche liegenden Projektionszentrum aus. Dadurch ist die Verzerrung zu den Rändern hin weniger extrem als bei der gnomischen Projektion. Die stereographische Azimutalprojektion wurde ebenfalls bereits von Hipparchos von Nicäa verwendet, aber zur Abbildung der Himmelskugel.

Transversale orthographische Azimutal­projektion 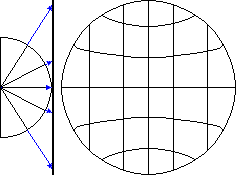Transversale gnomische Azimutal­projektion Polare stereographische Azimutal­projektion

Zylinderprojektionen

Bei der normalen Projektion ist die Zylinderachse parallel zur Erdachse, bei der transversalen Projektion steht die Zylinderachse normal zur Erdachse. Im einfachsten Fall der Normalen Projektion berührt der Zylindermantel die Erde am Äquator. Der Zylinder kann die Erde aber auch durchschneiden, der Mantel ist dann schmäler, die Landmassen erscheinen dadurch horizontal gestaucht. Der simpelste Fall einer Normalen Zylinderprojektion ist, die geographische Länge λ und Breite φ als kartesische Koordinaten zu verwenden (d.h. x = λ, y = φ). Längenkreise sind dann parallele Geraden, die Breitenkreise sind immer gleich lang. Die Projektion ist abstandsgetreu entlang der Meridiane (und entlang des Äquators), weist aber in Polnähe starke Flächenverzerrungen auf. Denn der Blick auf den Globus zeigt, dass Breitenkreise zu den Polen hin immer kleiner werden. Die Pole sind eigentlich Punkte, werden aber als Geraden, die sich über die ganze Karte erstrecken, abgebildet. So eine Karte nennt man Quadratische Plattkarte (oder mit einem frz. Ausdruck Plate carrée). Der Vorteil dieser Projektion ist, dass man Koordinaten einfach eintragen und ablesen kann. Sie soll bereits von Marinos von Tyros um 110 n.Chr. vorgeschlagen worden sein. Gerard de Kremer (latinisiert Gerardus Mercator) hatte die Idee, die Abbildung entlang der Zylinderachse zu strecken: y = ln [ tn (π/4 + φ/2) ] (vereinfacht). Das Geniale an der Mercatorprojektion: sie ist winkeltreu und Loxodromen werden als Geraden abgebildet. Um also auf See von A nach B zu navigieren, verbindet man die Punkte auf der Karte mit einem Lineal, misst den Winkel, unter dem diese Gerade die Meridiane schneidet, und hält genau diesen Winkel auf dem Kompass ein. Daher ist diese Projektion in der Seefahrt die Gebräuchlichste, und nach dem Wikipedia-Art. Mercator-Projektion (Stand Mai 2016) wird sie auch von Google Maps, Bing Maps, Openstreetmap usw. verwendet. (Wenn man sich die Tutorials zu Google MapMaker ansieht, hätte ich da eher auf die Orthographische Azimutalprojektion getippt.) In der Landvermessung wird ein auf der Transversalen Mercatorprojektion basierendes Koordinatensystem verwendet: das Gauß-Krüger-Koordinatensystem bzw. das jüngere UTM-Koordinatensystem (bei dem der Zylinder die Erdkugel geringfügig schneidet). Der Nachteil der Mercatorprojektion: die Flächenverzerrungen in Richtung auf die Pole sind noch extremer als bei der Plattkarte. Grönland erscheint auf Mercatorkarten etwa so groß wie Afrika. Im Prinzip läuft diese Projektion auf folgendes hinaus: wie bei der Plattkarte werden die im Pol zusammenlaufenden Meridiane als Parallelen abgebildet. Dadurch kommt es zu einer starken horizontalen Dehnung der Flächen zu den Polen hin. Um Winkeltreue zu gewährleisten, muss daher auch vertikal um einen entsprechenden Betrag gedehnt werden. In Mercators eigenen (etwas kryptischen) Worten in der Legende seiner Weltkarte von 1569: In marinis nauclerorum tabulis gradus longitudinum per omnes parallelos usque in polum crescunt supra sphaericam rationem, Auf den Seekarten der Schiffsherren wachsen die Längengrade über alle (Breiten-)Parallelen bis zu den Polen über die kugelförmige Weise hinaus. nam perpetuo aequales manent gradibus aequatoris, at gradus latitudinum minime crescunt, Denn sie bleiben stetig gleich groß wie die Grade des Äquators, aber die Breitengrade wachsen gar nicht. quare ibi quoque distrahi enormiter figuras regionum necesse est, et vel longitudines ac latitudines, vel directiones distantiasque a vero aberrare, [...] Deshalb werden dort auch notwendigerweise die Gestalten der Gebiete übermäßig auseinandergezogen und weichen die Längen und Breiten oder die Richtungen und Abstände von der Realität ab. quibus consideratis gradus latitudinum versus utrumque polum paulatim auximus pro incremento parallelorum supra rationem quam habent ad aequinoctialem, [...] Dieses bedenkend haben wir die Breitengrade zu beiden Polen hin allmählich vergrößert, entsprechend der Zunahme der Parallelen über das Maß hinaus, das sie am Äquator haben. hochaufgelöste Version der Karte bei der Bibliothèque nationale de France, Digitalisat der Begleittexte in Art. Mercator 1569 world map. Wikipedia, dt. Übersetzung und Erklärung in dem PDF Krücken, Friedrich Wilhelm: Ist das „Rätsel der (Konstruktion der) Mercator-Karte von 1569“ [Hermann Wagner] gelöst?. Die starke Zerdehnung in Polnähe macht auch klar, dass hier die Loxodrome um ein Vielfäches länger ist als die Orthodrome. Um riesige Umwege zu vermeiden, muss man hier anders navigieren. Eigenartigerweise hat Mercator seine Arbeit in dieser Richtung nicht fortgesetzt und es auch nie der Mühe für Wert erachtet, genauer zu erläutern, wie man seine Projektion herstellt. Der Logarithmus, der zur exakten mathematischen Beschreibung notwendig ist, war zu Mercators Zeit noch gar nicht entdeckt. Wenn man das Prinzip der orthographischen Projektion auf die Zylinderprojektion anwendet, erhält man die flächentreue Lambertsche Zylinderprojektion (x = λ, y = sin φ). Die Flächenverhältnisse sind zwar korrekt abgebildet, aber die Umrisse der Landmassen oder Grenzen sind zu den Polen hin wieder stark verzerrt (vertikal zusammengestaucht). Hier passiert also genau das Umgekehrte wie bei der Mercatorprojektion: Die Flächentreue wird gewährleistet, indem zu den Polen hin die Flächen vertikal immer stärker zusammengestaucht werden. Eine andere Form der orthographischen Projektion ist die 1974 von Arno Peters propagierte, auf James Gall zurückgehende, Gall-Peters-Projektion. Der Zylinder schneidet die Erdkugel bei 45°. Entlang dieser beiden Breitenkreise ist die Projektion abstandstreu. Da der Zylindermantel eine kürzere x-Achse aufweist, sind die Flächen im Vergleich zu Lamberts Zylinderprojektion horizontal gestaucht. (Dadurch ist die vertikale Stauchung zu den Polen hin etwas abgemildert.) Wie Jürgen Heyn auf seiner Seite Das Gall - Peters Missverständnis ausführt, ist Peters nach anderen Prinzipien und ohne Kenntnis der Gall-Projektion zu seiner Karte gekommen. Doch im Ergebnis sind sie einander so ähnlich, dass man sie als Spielarten desselben Prinzips betrachten kann.

Quadratische Plattkarte Mercatorprojektion. Sieht der gnomischen Projektion ähnlich, ist aber nicht mit ihr zu verwechseln. Lamberts Zylinderprojektion Gall-Peters-Projektion

Kegelprojektionen

Claudius Ptolemäus hat im 2. Jh. eine Projektion vorgeschlagen, bei der die Meridiane als Geraden abgebildet werden, die auf einen Punkt über dem Nordpol zulaufen, während die Breitenkreise als Kreisbögen dargestellt werden (sog. Erste Projektion des Ptolemäus). Dies entspricht im Prinzip einer Kegelprojektion. Als Verbesserung hat Ptolemäus vorgeschlagen, auch die Meridiane bogenförmig darzustellen, um der sphärischen Gestalt der Erdoberfläche besser Rechnung zu tragen (Zweite Projektion des Ptolemäus). Das nennt man eine pseudokonische Abbildung (unechte Kegelabbildung). Die im 16. Jh. aufkommende kordiforme (d.h. herzförmige) Projektion kann als Erweiterung der Zweiten Projektion des Ptolemäus aufgefasst werden. Die einschlägigen Bücher zum Thema Geschichte der Landkarte zeigen häufig auch Ptolemäus' Weltkarte o.ä., die einer Handschrift oder einem frühen Druck von Ptolemäus' Geographia entnommen sind. Ob allerdings Ptolemäus' Werk wirklich Karten enthalten hat, ist unklar, ja darf angesichts der Weise, in der in der Antike Bücher vervielfältigt wurden, bezweifelt werden. Für die meisten auf Kegelprojektion beruhenden Karten wird heute meist so vorgegangen, dass der Projektionskegel die Erdkugel schneidet. So entstehen zwei Breitenkreise, an denen die Projektion abstandstreu ist.

Gnomische Kegelprojektion Gradnetz der kordiformen Werner-Projektion, der Äquator in Rot. Als Vorlage verwendet habe ich: Urheber: Strebe.– Quelle: Wikipedia.– Lizenz: CC BY-SA 3.0.

Sonstige

In der Praxis verwendet man heute speziell für Weltkarten gerne ovale Projektionen, weil sie nicht so starke Verzerrungen aufweisen wie die Zylinderprojektionen. Zu diesen zählt die flächentreue Mollweideprojektion, die die Erde auf eine Ellipse abbildet und bei der der Pol ein Punkt ist. Oder man greift zu Projektionen, die einen Kompromiss zwischen Winkel- und Flächentreue darstellen. Beliebt sind z.B. die Robinson-Projektion (bei der Referenzpunkte definiert werden und die Punkte dazwischen dann interpoliert werden) oder die Winkel-Tripel-Projektion. Eine Übersicht darüber, was sonst noch möglich ist, findet man u.a.: Art. List of map projections. Wikipedia Map Projections. Wolfram MathWorld Radical Cartography

Gradnetz der Robinson-Projektion. Als Vorlage verwendet habe ich die Tissotsche Indikatrix derselben: Urheber: Eric Gaba ( Wikimedia Commons user: Sting).– Quelle: Wikipedia.– Lizenz: GFDL 1.2 und CC BY-SA 4.0 und älter.

Karten als Ausdruck der Weltsicht

Karten verzerren mehr oder weniger die Realität, weil sie nicht alle Aspekte der dreidimensionalen Wirklichkeit getreu wiedergeben können und weil Karten ja eine bewusste Abstraktion darstellen: die Landschaft enthält keine Beschriftungen; und für eine Straßenkarte sind andere Details relevant (z.B. Tankstellen) als für eine Wanderkarte.

Weltkarte Mercatorprojektion: Grönland erscheint so groß wie Afrika, die unsinnig riesige Landmasse der Antarktis habe ich überhaupt abgeschnitten.
Urheber: Wikipedia-User Jecowa?.– Quelle: Wikipedia.– Lizenz: GFDL 1.2 und CC BY-SA 3.0.– Bearbeitung: verkleinert, Gradnetz entfernt.

Gradnetz von Arno Peters' Weltkarte.
Urheber: Maximilian Dörrbecker, 2006.– Quelle: Wikimedia.– Lizenz: GFDL 1.2, CC BY-SA 3.0.– Bearbeitung: verkleinert, Antialiasing beim Gradnetz entfernt.

Arno Peters übte an der Mercatorprojektion heftige Kritik, weil sie angeblich die Bedeutung äquatornaher Dritte-Welt-Gebiete durch zu kleine Darstellung herunterspiele. Ob dieser Effekt tatsächlich besteht, ist dabei kaum festzustellen. (Irgendwo habe ich gelesen, dass in der Zeit des Kalten Krieges versucht wurde, die bedrohlich große Darstellung der Landmassen der UdSSR propagandistisch auszunutzen.) Die Flächenverzerrungen der Mercatorprojektion sind urspünglich nicht propagandistisch gemeint, sondern dem praktischen Zweck dieser Projektion geschuldet. Doch noch heute findet man im Netz lautstarke Attacken gegen die Mercatorprojektion.

Arno Peters hat seine eigene Projektion als politisch korrekte Darstellung der Dritten Welt verkauft. Seine Karte hat aber auch heftige Ablehnung hervorgerufen, weil der Grund für ihre Propagierung ein ideologischer war. Das Eigenartige an dieser Auseinandersetzung: warum sollte eine flächentreue Projektion eine richtigere Wiedergabe der Welt sein als z.B. eine abstandstreue? Nach Peters, weil Größe beim Betrachter automatisch Bedeutung evoziert. Aber Größe korreliert eben nicht mit der Bedeutung, auch nicht in der Realität. Was hilft es also, Flächenverhältnisse korrekt wiederzugeben?

Nicht erst seit der Zwischenkriegszeit wurde mit Karten auch Propaganda betrieben. Schon im 19. Jh. stellte etwa der britische Cartoonist Fred Rose auf einer Europakarte Russland als Kraken dar, der bereits Polen und Persien (in einer jüngeren Version zusätzlich Finnland) im Würgegriff hat und aktuell auch die Türkei bedroht, um sich das Kleinod an seinem Gürtel einzuverleiben: Istanbul und damit die Herrschaft über den Bosporus.

Aber interessanter finde ich, wie sich auf Karten die Weltsicht der Macher vielfach unbewusst oder zumindest unreflektiert offenbart. Jahrhunderte lang enthielten Karten aufwendig gestaltete Kartuschen und Randillustrationen, in denen nicht selten der Zweck der Karte oder der Standpunkt des Kartographen angedeutet oder offen ausgedrückt wird.

Imperial Federation, Map of the world showing the extent of the British empire in 1886.
Quelle: Wikimedia.– Lizenz: gemeinfrei.– Bearbeitung: stark verkleinert, Rot angehoben.

Auf den britischen Karten ihres Reiches wurde das zum Empire gehörende Gebiet rot eingefärbt, z.B. auf der Karte Imperial Federation von Walter Crane (1886). Die Welt wird so farblich unterteilt in Länder, die dazugehören, und Länder, die „draußen“ sind. Diese Usance wird bis heute beibehalten, s. z.B. The empire at its widest extent by 1921 vs. Today (2016). In gewisser Weise kann man das auch als Form thematischer Karte verstehen. Die Gleichung rot = britisch hat sich so fest in britische Hirne eingebrannt, dass der Protagonist in Joseph Conrads Roman Heart of Darkness (1899) sagen kann: „[...] on one end a large shining map, marked with all the colours of a rainbow. There was a vast amount of red — good to see at any time, because one knows that some real work is done in there [...]“ ([...] auf einer Seite eine große glänzende Landkarte, bemalt mit allen Farben des Regenbogens. Es gab eine riesige Menge Rot – jederzeit ein guter Anblick, weil man weiß, dass dort einige wirkliche Arbeit geleistet wird [...]) ( Text auf Wikisource).

Diese Karte von Walter Crane sagt auch sonst viel über das imperiale Selbstverständnis Britanniens: am unteren Bildrand sitzt Britannia mit dem Dreizack in der Hand auf einer Weltkugel, links und rechts von ihr pittoreske Tiere (Tiger, Elephant = Indien; Känguruh, Schafbock = Australien) und Menschen aus dem Empire (nordamerikanischer Indianer, indischer Elephantenführer, australische Aborigine). Sie symbolisieren den Reichtum und die Eintracht im Reich (s.a. die drei Wörter Freedom, Fraternity, Federation am oberen Rand).

Vor allem Beschriftungen sind ein hervorragendes Mittel, das politische Weltbild auszudrücken und Machtansprüche zu zeigen oder abzuweisen. So sind auf griechischen Karten der Türkei Instanbul und Izmir immer noch als Konstantinopel und Smyrna eingezeichnet, und die Republik Mazedonien (deren Name ja von Griechenland für sich beansprucht wird) ist ein namenloses Gebiet mit Skopje als Hauptstadt (s. Martin Belam: A Greek political map of Europe is also a map of the Greek political mindset).

Warum ist Norden oben?

Was zeichnet die Haupthimmelsrichtungen aus? Bei Osten und Westen sind es Sonnenauf- und -untergang. Der Osten als Ursprung des (Tages-)Lichts war auch für die christliche Welt lange Zeit die bevorzugte Himmelsrichtung. Daher sind auch (westliche) mittelalterliche Karten meist nach Osten, dem Orient, ausgerichtet, woher das Wort orientieren kommt. Umgekehrt wurde in manchen Kulturen (z.B. der ägyptischen) der Westen mit Tod assoziiert.

Norden und Süden sind als Kulminationspunkte des nächtlichen Sternenhimmels bzw. der Mittagssonne ausgezeichnet. Viele frühe Karten der islamischen Welt waren nach Süden ausgerichtet. Nach Brotton deswegen, weil für einen beträchtlichen Teil der Muslime die Richtung, in die sich sich beim Gebet wenden müssen, nämlich die Kaaba von Mekka, im Süden lag. Frühe chinesische Karten waren dagegen nach Norden ausgerichtet (genordet). Der Grund hierfür ist unbekannt. Denn auch für die Chinesen war eigentlich der Süden die bevorzugte Himmelsrichtung.

Dass auf den meisten europäischen Weltkarten der Norden oben und Europa mehr oder weniger in der Mitte der Karte ist, wird oft als gedankenloser – oder schlimmer noch: als imperialistischer – Eurozentrismus kritisiert. Doch eine Karte dient ja dazu, seinen eigenen Standpunkt in der Welt zu verorten, dazu muss man vom eigenen Zentrum ausgehen. Daher ist es nicht einfach nur kurios, wenn auf manchen australischen Weltkarten Süden oben und Australien in der Mitte ist; es ist vielmehr sinnvoll für Australier.

Karten müssten also nicht zwangsläufig genordet sein. Dies ist eine Usance, die sich erst in der frühen Neuzeit durchgesetzt hat, deren Ursprung nicht sicher zu bestimmen ist. Dass Karten eine Nord-Süd-Ausrichtung haben, liegt sicher am Aufkommen der Navigation mit Magnetkompass: die Nadel des Kompasses richtet sich entlang der in Nord-Süd-Richtung verlaufenden Magnetlinien aus (sie zeigt nicht nach Norden, wie man oft lesen kann). Es könnte aber auch der Süden oben liegen.

Kartendruck

Vor der Erfindung des Buchdrucks waren Karten mit mehr oder weniger großem Aufwand erstellte Zeichnungen, also Unikate. Das Kopieren einer Karte, die mehr war als eine einfache Skizze, erforderte größere Geschicklichkeit als das Abschreiben eines Textes. Daher bedeutete die Erfindung des Buchdrucks (Mitte des 15. Jh.) und die Möglichkeit der einfachen Vervielfältigung von Karten einen Quantensprung in der Verbreitung und Verwendung von Karten.

Die ersten Karten wurden als Holzschnitt ausgeführt: aus einer glatten Holzplatte wird alles, was weiß bleiben soll, herausgeschnitten. Die erhabenen Teile der Platte geben dann die Farbe an das Papier ab (Hochdruck). Eine bedeutende Karte, die in dieser Technik gedruckt wurde, war Martin Waldseemüllers Karte von 1507, eine aus zwölf Blättern bestehende, etwa 1,2 x 2,4 m große Wandkarte. Sie ist die älteste uns bekannte Karte, auf der der von Columbus entdeckte Kontinent als America betitelt ist. Ihr Gradnetz entspricht etwa der Zweiten Projektion des Ptolemäus, auf den sich der Kartentitel auch beruft. (Der Titel lautet: Universalis cosmographia secundum Ptholomaei traditionem et Americi Vespucii aliorumque lustrationes „Allgemeine Weltbeschreibung nach der Überlieferung des Ptolemäus und den Besichtigungen Amerigo Vespuccis und anderer“.)

Beim Kupferstich wird das Kartenbild mit einem Stichel in eine Kupferplatte graviert. Diese Vertiefungen nehmen beim Druck die Farbe auf und geben sie an das Papier ab (Tiefdruck). Der Kupferstich ermöglicht feinere Linien und Schraffuren als der Holzschnitt und löste diesen im 16. Jh. ab. Der niederländische Kosmograph Geert Kremer (der seinen Namen den Gepflogenheiten seiner Zeit entsprechend zu Gerardus Mercator latinisierte) war ein hervorragender Kupferstecher und realisierte seine Karten in dieser Technik, auch Mercators Weltkarte von 1569, für die er heute noch berühmt ist, die Nova et aucta orbis terrae descriptio ad usum navigantium emendate accommodata „neue und erweiterte Darstellung des Erdkreises, zum Gebrauch der Seefahrenden korrekt angepasst“. Diese bestand aus 18 Blättern und war ca. 2 x 1,25 m groß.

Auf Mercator geht auch der Begriff Atlas für eine Sammlung von Karten in Buchform zurück. Atlas ist bekanntlich in der griechischen Mythologie der Titanensohn, der das Himmelsgewölbe trägt. Der Begriff wurde gewählt in Anlehnung an Diodor, der infolge rationalistischer Mythendeutung Atlas für einen sternkundigen Weisen hielt, der die Kugelgestalt der Himmelsobjekte entdeckt habe (Diod. 3,60,2; 4,27,5). Mercators Atlas erschien posthum 1595. Als erster gedruckter Atlas wird allerdings das Theatrum Orbis Terrarum des Antwerpener Kartographen Abraham Ortelius aus dem Jahr 1570 betrachtet.

Im 17. Jh. wurde das Herstellen und Drucken von Karten zu einem lukrativen Geschäftsmodell. Aus dieser Zeit stammt der Begriff des Abkupferns: Karten, deren (meist nur auf einige Jahre anberaumtes) Schutzprivileg abgelaufen war, wurden von konkurrierenden Verlagen kopiert, oder man erwarb, wenn möglich, gleich die Druckplatten.

Im 19. Jh. ermöglichte die Lithographie erstmals mehrfarbige Drucke in großer Auflage. (Bis dahin mussten Karten von Hand koloriert werden.) Das Bild wird mit fetthaltiger Lithographietusche oder -kreide auf einen plan geschliffenen Kalkstein gezeichnet. Beim Drucken wird die fetthaltige Druckfarbe vom feuchten Stein abgewiesen, von den gezeichneten Partien aber aufgenommen und durch hohen Pressdruck aufs Papier übertragen (Flachdruck). Die Lithographie erfordert nicht soviel handwerkliches Geschick wie der Kupferstich und lässt sich viel schneller bewerkstelligen.

Heute wird durchgehend Offsetdruck verwendet. Er funktioniert ähnlich wie die Lithographie: auf einer eloxierten Aluminiumplatte wird auf den Stellen, die drucken sollen, ein Polymer aufgebracht. Die Platte wird beim Druck eingefeuchtet, die eloxierten Flächen weisen dann die Druckfarbe ab, die Stellen, auf denen das Polymer aufgetragen wurde, nehmen die Farbe an. Die Platte wird aber nicht direkt auf das Papier gedruckt, sondern über einen mit einem Gummituch bespannten rotierenden Zylinder. Erst von diesem Gummituch gelangt die Farbe aufs Papier.

Beachtenswerte frühe Karten

Hier sollen einige Karten vorgestellt werden, die aus der Zeit vor der Professionalisierung der Kartographie stammen. Vor allem zwei Faktoren haben im 16. Jh. diese Professionalisierung vorangetrieben: die Zunahme des geographischen Wissens durch die Entdeckungen spanischer und portugiesischer Seefahrer seit dem Ende des 15. Jh.; und der Buchdruck und die steigenden handwerklichen Fähigkeiten der involvierten Holzschneider und Kupferstecher.

Babylonische Weltkarte

Diese in den Ton geritzte und in babylonischer Sprache beschriftete Skizze ist, wie das Kolophon sagt, eine Kopie, ca. im 6. Jh. v.Chr. erstellt, deren Vorlage aber nicht älter als das 9. Jh. sein kann. Die Karte ist annähernd genordet. Sie ist keine Darstellung der realen Geographie des Babylonischen Reiches, sondern eine mappa mundi, d.h. eine Verortung Babylons im Kosmos, so wie man ihn sich damals vorstellte: Babylon ist der Nabel der Welt, durchflossen vom wichtigsten Strom, dem Euphrat; es ist allerdings nicht der Mittelpunkt der Karte, die durch ein Loch – vielleicht der Einstichpunkt eines Zirkels – kenntlich gemacht ist. Soweit die Bildfelder beschriftet sind, sind nur Armenien, das Zweistromland, die Susiana und das westliche Medien auszumachen; Ägypten, Syrien oder Anatolien scheinen zu fehlen. Dafür sind sieben (oder vielleicht acht) Zacken eingezeichnet, die ferne mythische Länder repräsentieren. Der (leider stark beschädigte) Text über der Zeichnung und auf der Rückseite scheint sich mit diesen Ländern zu beschäftigen (Nennung mythischer Personen, Aufzählung von exotischen Tieren oder Fabelwesen – die Unger allerdings für Sternbilder hielt).

Lat. mappa mundi bedeutet soviel wie „Weltkarte“ (lat. mappa „Tuch, Serviette“), vgl. frz. mappemonde ds. In der Kartographie bezeichnet man damit die mittelalterlichen Weltkarten, denen es weniger um Vermittlung exakter Geographie geht als vielmehr um die Darstellung der von Gott geschaffenen Ordnung.

Babylonische Weltkarte, BM 92687 (British Museum).
Urheber: Artaxiad (courtesy of the British Museum).– Quelle: Wikipedia.– Lizenz: gemeinfrei.– Bearbeitung: verkleinert, Text über der Zeichnung abgeschnitten.

Nachzeichnung mit der Numerierung von Horowitz. Blau: Wasser, lila: Stadt, grün: Land, Gebiet.

1: šadû „Gebirge“, d.i. Zagros?, Armenisches Hochland? 2, 11: URU (ālum) „Stadt“, vielleicht die ālānu abtutu „zerstörte Städte“, von denen im Text über der Zeichnung (Z. 2) die Rede ist; oder vielleicht war die Vorlage unleserlich geworden. 3: Urâštu „Urartu“, d.i. die Region um den Van-See (Armenien) 4: Aššur „Assyrien“ 5: Dêr, noch nicht lokalisierte Stadt an der Grenze zu Elam 6: [ma]rra[tum] „Meer“? [P]ura[ttu] „Euphrat“? [ḫa]rra[num] „Straße“? [qa]ra[ân tâmti] „Horn des Meeres“? 7: apparu „Schilfdickicht, Sumpf“ 8: Šuša „Susa“, Hauptstadt von Elam 9: bitḳu „Einschnitt, Kanal“ 10: Bîtiâkinu „Bit Jakin“, eine Region am unteren Euphrat 11: s. 2 12: Hâbban „Habban“, kleines Königreich der Kassiten (Bit Hamban/Habban) 13: Tintir „Babylon“ 14-17: marratum „Bitterstrom, Meer“, hier der Ozean, der die Erdscheibe umfließt 18: BÀD.GU.LA (dūrum rabum) „große Mauer“ (eine Bergkette, wie etwa der Kaukasus? eine kosmische Mauer am Ende der Welt?) 19-22: nagû „Landstrich, Gegend“, mythische Regionen am Rand der Welt? 23, 24, 25: ohne Beschriftung 26: Euphrat (ohne Nummer bei Horowitz)

Soleto-Karte (Mappa di Soleto)

Diese Karte, in die schwarzgrundige Scherbe eines (vermutlich rotfigurigen) Gefäßes des 5. Jh. v.Chr. geritzt, stellt die Küstenlinie und wichtigsten Orte der Südspitze Apuliens dar. Während die Echtheit der 2003 in Apulien gefundenen Scherbe unbezweifelt ist, wird die Karte von manchen für einen Wissenschaftlerscherz gehalten. Die Nordung der Karte, die Darstellung der Städte durch einen Punkt, das Fehlen von Verkehrsverbindungen und die Ähnlichkeit mit der Darstellung der Region in einem niederländischen Schulatlas gaben Anlass, an der Authentizität zu zweifeln.

Tabula Peutingeriana

Ausschnitt aus Konrad Millers Faksimile der Tabula Peutingeriana: Mittel- und Süditalien, Sizilien; über dem italienischen Stiefel ist die Adria und die Küste Dalmatiens und Albaniens, unter ihm das Tyrrhenische Meer und die Kleine Syrte und die tunesische Küste. Ganz links die Vignetten Roms und Ostias, direkt darunter Karthago (!).
Quelle: Wikimedia.– Lizenz: gemeinfrei.

Ausschnitt aus Konrad Millers Faksimile der Tabula Peutingeriana: Links unten Ivavo (Salzburg), von dem aus eine Straße in drei Tagesetappen nach rechts oben nach Ovilia (d.i. Ovilava, Wels) führt. Darunter die Straße ins Salzachtal und über die Niederen Tauern nach Kärnten.
Quelle: Wikipedia.– Lizenz: gemeinfrei.– Bearbeitung: leicht vergrößerter Ausschnitt, Sättigung reduziert, aufgehellt.

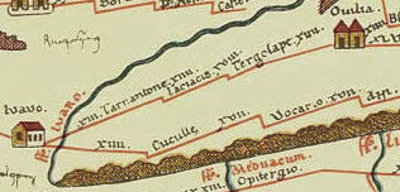
Die nach einem ihrer Vorbesitzer, dem Augsburger Stadtschreiber und Humanisten Konrad Peutinger (1465-1547), benannte Rollkarte ist 34 cm hoch, 6¾ m lang und besteht aus 11 Blättern. Sie zeigt das Straßennetz des Römischen Reiches der Spätantike, mit Städten und Pferdewechselstationen, Entfernungsangaben und Angabe von Tagesetappen. Sie reicht heute von Gallien bis nach Indien und Zentralasien (der westlichste Teil – Britannien und die Iberische Halbinsel – ist offenbar verloren gegangen), einschließlich Nordafrika und den Nahen Osten. In ihrer extremen Stauchung nimmt sie in manchem das Konzept der modernen Netzspinne (Liniennetzplan) vorweg. Da sie von West (links) nach Ost (rechts) geht, könnte man sagen, sie ist ungefähr genordet. Doch die Landmasse Italiens liegt horizontal, Kreta ist auf gleicher Höhe wie die Peloponnes, d.h. hier ist Nordosten oben. Auch in der Verwendung von Piktogrammen zur Klassifizierung der Etappenziele und Ortschaften nimmt die Karte neuzeitliche Konzepte vorweg.

Die klassische Netzspinne entwickelte der Grafikdesigner Harry Beck 1933 für die Londoner U-Bahn (man vgl. die herkömmliche Tube map 1926 mit der Beck Map 1933).

Das spätantike Original dürfte in der zweiten Hälfte des 4. Jh. angefertigt worden sein: die Karte enthält bereits Constantinopolis, wie Byzántion seit 337 offiziell heißt. Sie dürfte aber deutlich ältere Vorlagen verwendet habe: auch die 79 vom Vesuv verschütteten Städte Pompeji, Herculaneum, Stabiae und Oplontis sind noch verzeichnet. Diese Karte ist wohl in der Karolingerzeit kopiert worden. Diese Kopie wiederum ist im 12. Jh. abgezeichnet worden, unsere Tabula. Sie wurde 1494 von Conrad Celtis entdeckt und 1507 an Konrad Peutinger übergeben. Nach Peutingers Tod ließ der Augsburger Humanist Markus Welser (1558-1614) ein Faksimilie zum Behuf des Drucks erstellen. Dieses wurde 1598 in Antwerpen gedruckt, 1624 als Anhang in der letzten Ausgabe des Theatrum Orbis Terrarum nachgedruckt. 1887 fertigte der katholische Theologe Konrad Miller (1844-1933) ein neues Faksimile und hat dabei auch versucht, den fehlenden Teil zu rekonstruieren. Das Original liegt in der Österreichischen Nationalbibliothek (Codex Vindobonensis 324).

Über den Zweck der Karte mag Oswalt in der Sache Recht haben, wenn er urteilt: „[...] lässt sie sich primär als Propaganda für die Römische Reichsidee, die Pax Romana, interpretieren.“ (S. 72) Doch als Fazit erscheint mit das zu seicht. Interessant ist, was die Karte darstellt und was nicht. Sie zeigt die damals bekannte Oikumene als Geflecht aus Straßen und Etappenorten, auch hierin einem Liniennetzplan vergleichbar. Sie ist offenbar nicht interessiert an der korrekten Wiedergabe von Flächenverhältnissen oder Küstenlinien (zwischen Ostia und Karthago passt nicht mehr als ein Daumen), oder an Schifffahrtsrouten. Der römische Pragmatismus zeigt sich auch daran, dass sich die Karte keinen Spekulation darüber hingibt, was an den Rändern oder darüber hinaus sein könnte. Man vgl. im Gegensatz dazu etwa mittelalterliche Karten wie die Ebstorfer Weltkarte (s.u.) oder auch frühe neuzeitliche Karten. Auch wenn die Karte keinem praktischen Zweck gedient haben sollte, legt sie ein beredtes Zeugnis von der Zweckorientierung römischer Kartographie ab.

Mosaik von Madaba

Jericho und seine Umgebung auf dem Mosaik von Madaba: unten die palmengesäumte Oasenstadt, in der Mitte rechts die Einmündung des Jordan in das Tote Meer.–
Urheber: M. Disdero, 2007.– Quelle: Wikimedia.– Lizenz: CC BY-SA 2.5.– Bearbeitung: Bildausschnitt, verkleinert, geschärft, automatischer Abgleich.

In der St.-Georgskirche in Madaba (Jordanien, ca. 25 km südwestl. von Amman, schon im AT als מֵידְבָא Mêd^ebâ bekannt) befindet sich ein großflächiges Mosaik (ursprl. etwa 21 x 7 m), das eine Karte des Heiligen Landes darstellt. Auf Grund der Bauwerke, mit denen Jerusalem dargestellt ist, kann diese Karte auf die Mitte des 6. Jh. datiert werden. Die Karte ist nach Osten ausgerichtet, sodass die Himmelsrichtungen auf ihr mit den tatsächlichen ungefähr übereinstimmen. Von der ursprünglichen Mosaikfläche ist weniger als die Hälfte erhalten.

Die Darstellung erstreckte sich vom Libanon (?) bis zum Nildelta, vom Mittelmeer bis Transjordanien. Sie zeigte neben den wichtigen Städten wohl vor allem Ziele christlicher Pilger. Als Quelle dürfte Eusebius' Onomastikon gedient haben.

Die besser erhaltenen Mosaike in der St.-Stefanskirche in Umm ar-Raṣāṣ (Jordanien, 50 km südl. von Amman) sind zwei Jahrhunderte jünger als die in Madaba und zeigen vereinfachte Stadtansichten, darunter von Midaba (=Madaba), Esbounta (=Hešbon), Philadelphia (=Amman), „die heilige Stadt“ (=Jerusalem), Neapolis (=Sichem, h. Nablus), Kesaria (=Caesarea), Askalon, Sebastis (=Samaria?) u.a.

T-O-Karten

Geostete T-O-Karte (Oriens „Osten“ ist oben, Sepentrio „Norden“ links): die Erde ist umflossen vom Mare Oceanum „Ozeanisches Meer“, die drei Kontinente sind geteilt durch das Mare magnum sive mediterraneum „großes oder mittelländisches Meer“. Jeder Kontent wird hier einem der drei Söhne Noahs (Sem, Ham, Japhet) zugeteilt (d.h. ist von deren Nachkommen bewohnt). Aus der ersten gedruckten Ausgabe von Isidor von Sevillas Etymologiae (Augsburg: Günther Zainer, 1472), vermutlich die älteste gedruckte Karte überhaupt.
Quelle: Wikipedia.– Lizenz: gemeinfrei.– Bearbeitung: verkleinert und zum besseren Verständnis koloriert.

Viele mittelalterliche Weltkarten sind nach dem Schema der T-O-Karte ausgeführt. Das T steht für das Mittelmeer (senkrechter Balken), den Don (und das Schwarze Meer) (linker Balken) und den Nil (oder das Rote Meer) (rechter Balken), die die Erde in die Kontinente Europa, Afrika und Asien teilen; das O für den Ozean, der nach antiker Vorstellung die Erde ringförmig umgibt. Meist sind diese Karten nach Osten ausgerichtet.

Diese Karten sind, auch wenn sie mit vielen Details, Ländernamen, Flüssen, Städten usw. gefüllt sind, mappae mundi. Sie dienen zur Illustration oder zur Repräsentation, meist im Zusammenhang mit dem christlichen Glauben.

So ist die Beatuskarte eine Illustration im Kommentar zur Johannes-Apokalypse, der um 776 von dem Mönch Beatus von Liébana (Nordspanien) verfasst wurde: vor der Kommentierung von Offb 2 und 3 (Sendschreiben an die sieben Gemeinden Kleinasiens) wird in einem Prolog von den zwölf Aposteln und den Ländern und Weltteilen berichtet, die diese missionierten. Diese Karte ist in unterschiedlicher Gestalt in Handschriften des 10. bis 13. Jh. überliefert.

Die Ebstorfer Weltkarte ist eine im Benediktinerinnenkloster von Ebstorf (Lüneburger Heide) gefundene und wohl auch dort um 1300 hergestellte Großkarte mit 3,5 m Seitenlänge. Das Original ist 1943 bei einem Luftangriff auf Hannover verbrannt. In der Karte sind auch Orte und Ereignisse aus der Bibel (Paradies und Sündenfall, Landung der Arche Noah, Turm von Babel), der antiken Mythologie (Amazonen, Phönix) und dem legendenhaften Alexanderroman (die menschenfressenden Völker Gog und Magog), sowie zahlreiche Tiere eingezeichnet. An den vier Seiten sind Christi Kopf, Hände und Füße zu sehen. Christus umfasst gleichsam schützend die Erde. „Heilsbotschaft und enzyklopädisches Weltwissen vereinigen sich zu einem christlichen Weltbild [...], in dem alles seinen festen Platz in der gottgewollten Ordnung besitzt.“ (Oswalt S. 87). Wie auch auf vielen anderen Karten des Mittelalters bildet Jerusalem das Zentrum der Karte. Das T-O-Schema ist nicht auf den ersten Blick zu erkennen. Auch hier wird die obere Hälfte zum Großteil von Asien eingenommen. Doch ist der rechte Balken des T steil noch oben gerichtet, wodurch Afrika die Form eines Kreissegments hat. Oder anders gesagt: das T sieht wie um 90° im Uhrzeigersinn gedreht aus. Die Karte diente wohl als Kirchenschmuck für hohe Feiertage.

Ähnlich gestaltet ist die Hereford-Karte. Sie ist mit ca. 135 cm Durchmesser die größte noch vollständig erhaltene mittelalterliche Karte. Sie wurde Ende des 13. Jh. im Auftrag des späteren Domherren von Hereford (Westengland), Richard von Haldingham oder von Lafford, wie er in der linken unteren Ecke der Karte genannt wird, angefertigt und wird heute in der Hereford Cathedral aufbewahrt. Aus unerfindlichen Gründen sind die Beschriftungen von Afrika und Europa vertauscht, d.h. Afrika ist mit Europa beschriftet und Europa mit Affrica. An den vier Nebenhimmelsrichtungen finden sich, beginnend im Nordosten, im Uhrzeigersinn die Buchstaben M-O-R-S, das lat. Wort für „Tod“. Am Kopf der Karte ist das Jüngste Gericht mit Christus als Weltenrichter dargestellt.

Diese Karten entspringen keiner wissenschaftlichen Intention. Sie haben kein Gradnetz, und die Topographie (Küstenlinien, Lage von Orten und Ländern usw.) ist nur sehr schematisch und approximativ wiedergegeben. Sie dienen vielmehr der Verortung und Illustration wesentlicher biblischer Geschehnisse.

Die letzte bedeutende im Stil der (T-)O-Karten verfertigte Karte ist das Werk eines venezianischen Mönchs aus den 1450er Jahren: die Karte des Fra Mauro. Die Karte hat eine Größe von 2.4 mal 2.4 m, sie ist nach Süden orientiert und hat die Entdeckungen der Reisenden und Seefahrer ihrer Zeit eingearbeitet. Die Umrisse von Ländern und Kontinenten nähern sich bereits der Realität. Amerika fehlt natürlich noch. Aber es fehlen auch die typischen Elemente früherer mappae mundi wie das Paradies am Ostrand oder Fabelwesen wie Menschenfresser, Cynocephali (Hundsköpfige), Troglodyten (Höhlenbewohner), Menschen mit riesigen Unterlippen, die sie als Sonnenhut verwenden können, usw.

Portolankarten

In der Antike gab es die Literaturgattung des Periplus (griech. περίπλους „Umsegelung; Herumsegeln, Fahrt“), eine Beschreibung von Küsten, Landmarken, Häfen, Entfernungen, Möglichkeiten zur Versorgung mit Wasser und Proviant usw. Diese dienten als Navigationshilfe für die Seefahrer.

Eine ganz ähnliche Art von „geschriebener Karte“ hieß im Spätmittelalter Portolan (it. portolano von lat. portus „Hafen“). Diese wurden dann auch mit Karten illustriert, die man heute Portolankarten nennt. Typisch für Portolankarten sind die vielfach sich überkreuzenden sog. Rumbenlinien (Sehnenlinien, Windstrahlenbüschel). Das sind farbige Linien, die von über die Karte verteilten Windrosen ausgehen und die Navigation mit dem Kompass erleichtern sollten (v. span. rumbo „Kurs, Richtung“?). (Vielleicht dienten die Linien aber auch als Hilfe für die Kartenkopisten.)

Bedeutende Portolankarten sind etwa:

• Karte Westeuropas von Pietro Vesconte (1325)
• die Karten des Katalanischen Atlas von Abraham Cresques (1375), sechs zweiseitige, je 64 x 50 cm große Karten, die vom Atlantik bis China reichen
• die Portolankarte des Albino de Canepa (1489), eine Karte des Schwarzen Meeres, des Mittelmeers und der europäischen Atlantikküste
• die berühmte Karte des Pīrī Reʾīs (1513), eine osmanische Karte des Atlantiks, die interessanterweise auch den Küstenverlauf Amerikas zeigt, obwohl die Osmanen niemals dort waren

Lucas Cranachs Karte des Heiligen Landes

Ein Anliegen der Reformation war, dass jeder Gläubige die Bibel lesen und verstehen sollte. Als ein Hilfsmittel dazu wurden u.a. Karten betrachtet. Daher enthielten gedruckte Bibelausgaben schon früh Landkarten als Beigabe. Die erste Karte in einer Bibelausgabe war eine Karte des Heiligen Landes in Luthers Altem Testament, gedruckt 1525 von Christoph Froschauer in Zürich. Die Karte ist nur annähernd genordet (sie verläuft von NW nach SO), aber seitenverkehrt (Osten ist links). Sie zeigt das Land aus der Vogelperspektive, von Damaskus bis zum Sinai, vom Ostrand Ägyptens (Sukkot) bis zur Syrischen Wüste. Im Vordergrund ist comic-strip-artig der Exodus der Israeliten dargestellt. Dieselbe Karte erschien, ins Niederländische übersetzt und seitenrichtig, bereits 1526 bei Jacob van Liesveldt in Antwerpen und mit geringen Änderungen 1528 bei Willem Vosterman in Antwerpen.

Bei der Karte in Froschauers Bibel handelt es sich um eine verkleinerte Kopie eines Holzschnitts von Lucas Cranach d. Ä. Cranachs Karte muss zwischen 1508 und 1524 entstanden sein. Das noch erhaltene Exemplar, bei dem allerdings am unteren Rand ein schmaler Streifen fehlt, ist 60 x 52 cm groß. Die Karte ist ein Mittelding zwischen einer Karte und einer Bibelillustration. Warum der Holzschneider für Froschauers Ausgabe nicht daran gedacht hat, seine Vorlage zu spiegeln, ist unklar. Liesfeldts Karte ist eine Kopie der Froschauerschen Version.

Eine ähnliche Karte war auch in der englischen Bibelausgabe von Miles Coverdale aus dem Jahr 1535 zu finden. Allerdings ist ihre Orientierung umgedreht (von SO nach NW), der Zug der Israeliten durch das Schilfmeer ist im Hintergrund (oben rechts) zu sehen. Während die Perspektive der Karte sehr an Cranachs Karte erinnert, ist die Geographie wohl angelehnt an zwei Karten von Jakob Ziegler, die dieser seiner offenbar titellosen geographischen Schrift, Straßburg 1532, beigeben hatte. (Der zitierte Titel Quae intus continentur. Syria, ad Ptolemaici operis rationem [...]. Palestina [...] ist die Inhaltsangabe: „was im Inneren enthalten ist: Syrien, nach der Weise des Ptolemäischen Werkes [...]. Palästina [...]“.)

Seltsame Orte

Thule

Das sprichwörtliche ultima Thula „äußerstes Thule“ (griech. Θούλη) (nämlich im äußersten Norden der Oikumene) wurde erstmals von dem griechischen Entdecker Pytheas aus Massilia im 4. Jh. v.Chr. beschrieben . Es ist eine Insel, die sechs Tagesreisen nördlich des nördlichen Britannien und eine Tagesreise vom „geronnenen Meer“ (wohl dem Eismeer) entfernt liegen soll. Pytheas Werk ist leider nur noch in Zitaten bei Strabon, dem älteren Plinius u.a. erhalten. Es ist unklar, welches Land Pytheas genau meinte. Kandidaten für sein Thule sind die Färöer, Island oder Mittelnorwegen (z.B. die Insel Smøla). Die Lofoten liegen m.E. schon zu weit nördlich, um in Frage zu kommen.

Die Römer, die nach Tacitus am Ende von Agricolas Kaledonierfeldzugs 83 n.Chr. die Orkney-Inseln umsegelten, identifizierten ein nördlich davon gesichtetes Land mit Thule, vermutlich die Shetland-Inseln. Das Thule, in das nach Prokopios ein Teil der Heruler nach ihrer Niederlage gegen die Langobarden zogen und das zehnmal so groß wie Britannien sein soll, wird wohl Skandinavien sein.

Die Bezeichnung Skandinavien geht auf antike Autoren zurück, die Gebiete im Norden Europas mit einem Namen nennen, der mit skand- beginnt: Plin. nat. 4,(13,27) 96 Scatinavia bzw. 8,(15) 39 Scadinavia, und 4,(16,30) 104 Scandia(e) (aber wohl nicht dasselbe), Ptol. geogr. 2,10 (11), 33-35 Skandía, Iord. Get. 1 (9), 3 (16) et passim Scandza. Der Name wird german. Ursprungs sein, es wurden verschiedene Etymologien vorgeschlagen, etwa zu ahd. scado, got. skaþis „Schaden“.

Säulen des Herakles

Als Säulen des Herakles bezeichnete man in der Antike zwei Vorgebirge links und rechts der Straße von Gibraltar, nämlich Kalpe, d.i. der Felsen von Gibraltar, und Abila, d.i. der Dšebel Musa in Marokko (nach anderen der Monte Hacho in der spanischen Enklave Ceuta). Die Meerenge von Gibraltar war für die griechischen Seefahrer lange Zeit die westliche Grenze der bekannten Welt.

Der Name Gibraltar bezeichnet die Halbinsel an der Südspitze Spaniens. Er ist nach vorherrschender Meinung span. Verballhornung des arab. ǧabal Ṭāriq „Berg des Tariq“ (näml. des Ṭāriq ibn Ziyād, eines muslimischen Berbers, der von hier aus ab 711 Spanien eroberte.)

Kap der Guten Hoffnung

Das Kap der Guten Hoffnung ist das bekannte und gefährliche Kap nahe der Südspitze Afrikas. Diese Südspitze wurde 1488 von dem portugiesischen Seefahrer Bartolomeu Dias als erstem neuzeitlichen Europäer umsegelt. Dias hatte es Cabo das Tormentas „Kap der Stürme“ genannt; es war wohl der portugiesische König Johann II., der es in Cabo da Boa Esperança umbenannte. Dias wurde allerdings von seiner Mannschaft zum Umkehren gezwungen. Vasco da Gama erreichte dann auf diesem Kurs 1498 erstmals Indien.

Die Umsegelung der Südspitze Afrikas war schon in der Antike versucht worden. Nach Herodot (4,42) war sie den Phöniziern im Auftrag Pharao Nechos um 600 v.Chr. (im Uhrzeigersinn) gelungen. Eudoxos von Kyzikos im 2. Jh. v.Chr. dürfte hingegen (gegen den Uhrzeigersinn) erfolglos geblieben sein. Ptolemäus war dann der Meinung, dass eine Landverbindung zwischen dem südlichen Afrika und Ostasien bestehe und der Indische Ozean somit keine Verbindung zum Atlantik habe. Dias' und da Gamas Umsegelung eröffnete den Seeweg nach Indien und Fernost. Der Weg um das Kap verlor seine Bedeutung erst durch die Öffnung des Suezkanals.

Inseln der Seligen

Die Bezeichnung geht zurück auf den im Griech. Inseln der Seligen genannten Aufenthaltsort der Verstorbenen, die rein und gerecht gelebt haben (so z.B. bei Pind. O. 2,70ff) oder von den Göttern dafür auserkoren wurden, ungefähr gleichbedeutend mit dem Elysium. Diesen stellte man sich ursprünglich an den Enden der Erde im Okeanos liegend vor. Die von Plinius (Plin. nat. 6,202-205) als Fortunatae insulae „glückselige Inseln“, von Plutarch (Plut. Sert. 8) als νῆσοι Μακάρων „Inseln der Seligen“ beschriebenen, im Atlantik gelegenen Eilande werden meist mit den Kanarischen Inseln gleichgesetzt, aber auch die Azoren, Madeira oder die Kapverdischen Inseln wurden in Betracht gezogen.

Hier wurde also der Name mythischer Inseln auf tatsächlich existierende Inseln, von denen man allerdings nur undeutliche Kunde hatte, übertragen. Diese Inseln finden sich auf vielen Karten des Mittelalters und der frühen Neuzeit, z.B. Beatuskarte (insulae fortunatarum), Hereford-Karte (fortunate isulee), Waldseemüllerkarte (insule fortunate) u.ä.

Weniger klar ist die Sache bei der St.-Brendan-Insel, einer Insel im Atlantik, die der irische Klostergründer St. Brendan bei einer Seereise im 6. Jh. entdeckt haben soll. Zwar ist der Bericht darüber, die Navigatio Sancti Brendani, eine auf keltischen Mythen basierende Erzählung aus dem 9. Jh., aber es ist auch nicht auszuschließen, dass hinter der Beschreibung der Insel Erinnung an Reales steckt, vielleicht ebenfalls eine der Kanaren. Doch wird die Insel heute mehrheitlich als Phantominsel betrachtet.

Syrte

Das Mittelmeer zwischen Kreta und Karthago und die beiden Syrten.– Urheber: Meyers historischer Handatlas, Leipzig 1911, Karte 17 (Das römische Weltreich um die Mitte des 2. Jahrhunderts n. Chr.).– Quelle: Archive.org.– Lizenz: gemeinfrei.– Bearbeitung: gedreht, ausgeschnitten, verkleinert, die Syrten farblich hervorgehoben, einige Beschriftungen hinzugefügt.

Als das Schiff, auf dem der Apostel Paulus nach Rom gebracht werden soll, nach dem Ablegen von Kreta in ein schweres Unwetter gerät und nicht mehr gesteuert werden kann, „lassen sie das Gerät hinab“, weil sie befürchten, sonst in die Syrte zu getrieben zu werden (Apg 27,17b). (Manche verstehen das so, dass die Segel eingeholt werden, andere, dass Treibanker ausgeworfen werden.) Die Syrten sind zwei Buchten an der Küste Afrikas: die Große Syrte vor der Küste Libyens zwischen Bengasi und Mis(u)rata, die Kleine Syrte vor der Küste Libyens und Tunesiens zwischen Tripolis und Kap Bon (nach Wikipedia nur zwischen der Insel Djerba und Sfax).

Die Syrten waren in der Antike bei Seeleuten gefürchtet wegen der unberechenbaren Strömungen und der Sandbänke. Herodot ist der erste antike Autor, der die (Große) Syrte nennt, aber noch ohne ihre Gefährlichkeit zu thematisieren (2,32,2; 2,150,1; 4,169,2; 4,173). Lateinische Dichter nennen sie gern in einem Atemzug mit Skylla und Charybdis. Hier ein kleines Florilegium:

Lucanus schließlich gibt folgende Beschreibung (9,303-318), nach der die Syrte ein Zwitter zwischen Meer und Land ist. Sei es weil sie von der Natur „unfertig“ erschaffen wurde, sei es weil sie, ursprünglich Meer, dabei ist auszutrocknen.

Im folgenden beschreibt Lucanus dann, wie Catos Flotte in die Syrte fährt, dabei aber ein Sturm aufkommt und ein Teil der Schiffe auf Sandbänke aufläuft.

Autor: Michael Neuhold (E-Mail-Kontakt)
Letzte Aktualisierung: 2. Mai 2021